Solve.The average value of a certain type of automobile was $14,220 in 1992 and depreciated to $6660 in 1995. Let y be the average value of the automobile in the year x, where x = 0 represents 1992. Write a linear equation that relates the average value of the automobile, y, to the year x.
A. y = -2520x - 900
B. y = -2520x + 14,220
C. y = -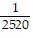 
x - 6660
D. y = -2520x + 6660
Answer: B
You might also like to view...
Find the derivative.g(x) = 3x2e-x
A. 3xe-x(2 - x) B. 3xex(2 - x) C. 3xe-x(x + 2) D. 6xe-x(1 - x)
Find the derivative of the function.y = log3
A.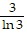 
B.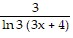 
C.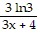 
D. 
Simplify the expression.
A. 2?y? - 8 B. ?2y - 8? C. 2y - 8 D. -2y + 8
Solve the problem.On a Touch-Tone phone, each button produces a unique sound. The sound produced is the sum of two tones, given by y = sin (2?lt) and y = sin (2?ht)where l and h are the low and high frequencies (cycles per second) shown on the illustration.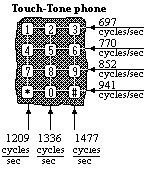
The sound produced is thus given by y = sin (2?lt) + sin (2?ht)Write the sound emitted by touching the 8 key as a product of sines and cosines.
A. y = 2 sin(2188?t) cos(484?t) B. y = 2 sin(625?t) cos(2329?t) C. y = 2 sin(484?t) cos(2188?t) D. y = 2 sin(2329?t) cos(625?t)