Solve the inequality.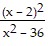
> 0
A. (-?, -6) or (6, ?)
B. (-6, 2) or (2, 6)
C. (-6, 2) or (6, ?)
D. (-?, -6) or (2, 6)
Answer: A
You might also like to view...
Find the amplitude, period, or phase shift of the given function as requested.Find the amplitude of y = 5 cos 
.
A. -5
B. -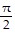 
C.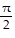 
D. 5
Completely factor the polynomial or state that the polynomial is prime.10(x - 2)2 - 7(x - 2) - 12
A. (2x + 8)(5x + 13) B. (2x + 3)(5x + 4) C. (2x + 5)(5x + 6) D. (2x - 7)(5x - 6)
Solve the problem.The graph depicts a person's speed y, in miles per hour, during a 15-minute period of driving. The graph has two turning points.The first turning point is the point at which the graph stops rising and starts to fall. The second turning point is the point at which the graph stops falling and starts to rise again. Estimate and interpret the turning points.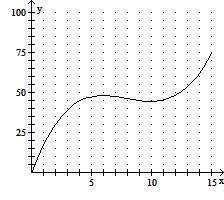
A. The first turning point is at approximately (6, 48). This is where the person's distance from the starting point stops increasing and starts to decrease. The second turning point is at approximately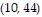 
. This is where the person's distance from the starting point stops decreasing and starts to increase again.
B. The first turning point is at approximately (5, 48). This is where the person's distance from the starting point stops increasing and starts to decrease. The second turning point is at approximately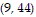 
. This is where the person's distance from the starting point stops decreasing and starts to increase again.
C. The first turning point is at approximately (6, 48). This is where the person's speed first stops increasing and starts to decrease. The second turning point is at approximately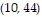 
. This is where the person's speed stops decreasing and starts to increase again.
D. The first turning point is at approximately (7, 48). This is where the person's speed first stops increasing and starts to decrease. The second turning point is at approximately (11, 44). This is where the person's speed stops decreasing and starts to increase again.
Find the general solution for the differential equation.x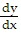
- 2y - 6x = 0
A. y = -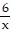 
+ C
B. y = -6 + Cx
C. y = -6x + Cx2
D. y = -6x2 + Cx3