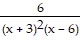Solve the problem.
= ky + f(t) is a population model where y is the population at time t and f(t) is some function to describe the net effect on the population. Assume k = .02 and y = 10,000 when t = 0. Solve the differential equation of y when f(t) = 5t.
A. y = 250t - 12,500 + 22,500e-.02t
B. y = 250t + 12,500 + 22,500e-.02t
C. y = -250t - 12,500 + 22,500e-.02t
D. y = -250t - 12,500 + 22,500e.02t
Answer: D
You might also like to view...
If the function is one-to-one, list the inverse function by switching coordinates or inputs and outputs.f = {(5, 5), (-5, -5), (8, 1), (-8, -1)}
A. f-1 = {(5, 5), (-5, -5), (1, 8), (-1, -8)} B. f-1 = {(-1, 8), (-5, -5), (5, -5), (1, -8)} C. not one-to-one D. f-1 = {(-1, 8), (8, -5), (5, 5), (1, -8)}
Solve the problem.Use the formula N = Iekt, where N is the number of items in terms of the initial population I, at time t, and k is the growth constant equal to the percent of growth per unit of time. A certain radioactive isotope decays at a rate of 0.2% annually. Determine the half-life of this isotope, to the nearest year.
A. 3 years B. 347 years C. 250 years D. 151 years
Solve the problem.If it has been determined that the probability of an earthquake occurring on a certain day in a certain area is 0.01, what are the odds against an earthquake?
A. 1 to 100 B. 100 to 1 C. 98 to 1 D. 99 to 1
Find the LCD of the rational expressions. Then rewrite each as an equivalent rational expression with the LCD.
; 
A.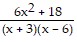 
; 
B. 
; 
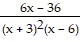
C.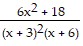 
; 
D.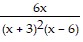 
; 