Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.Show that the formula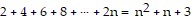 
obeys Condition II of the Principle of Mathematical Induction. That is, show that if the formula is true for some natural number k, it is also true for the next natural number 
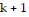. Then show that the formula is false for 
.
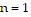What will be an ideal response?
Assume the statement is true for some natural number k. Then
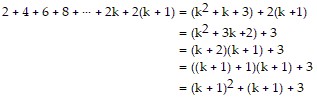
So the statement is true for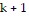 
.
However, when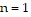 
, the left side of the statement is 
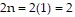, and the right side of the statement is 
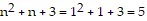, so the formula is false for 
.
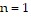You might also like to view...
Use Euler's method with given values of n to obtain an approximation of the initial value problem when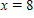 
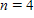
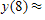
. Round your answers to four decimal places, if necessary.
?
, 
?
, 
__________
?
, 
__________
What will be an ideal response?
Solve the system of equations by substitution. x + 2y = 23x - 7y = -7
A. (1, 1) B. (0, 0) C. (1, 0) D. (0, 1)
The graph shows the pressure experienced by an ocean diver at two different depths. Find and interpret the midpoint of the line segment shown in the graph.
 figure 2.png)
Solve the problem.A business estimates that the salvage value V of a piece of machinery after t years is given by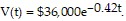 
After what amount of time will the salvage value be $639?
A. After 9.6 years B. After 10.6 years C. After 11.6 years D. After 8.6 years