Use mathematical induction to prove the following.If a is a constant and 0 < a < 1, then an < 1.
What will be an ideal response?
Answers may vary. One possibility:
Sn: If a is a constant and 0 < a < 1, then an < 1.
S1: If a is a constant and 0 < a < 1, then a1 < 1.
Sk: If a is a constant and 0 < a < 1, then ak < 1.
Sk+1: If a is a constant and 0 < a < 1, then ak+1 < 1.
1. Basis step: Since it is given that a < 1, then a1 < 1. Therefore, S1 is true.
2. Induction step: Let k be any natural number. Assume Sk. Deduce Sk+1.
If a is a constant and 0 < a < 1, then ak < 1.
If a is a constant and 0 < a < 1, then ak ? a < 1 ? a. Multiplying by a, a > 0
If a is a constant and 0 < a < 1, then ak+1 < a.
If a is a constant and 0 < a < 1, then ak+1 < a < 1. Given a < 1
If a is a constant and 0 < a < 1, then ak+1 < 1.
You might also like to view...
Graph the function.h(x) = x3 + 3
A. 
B. 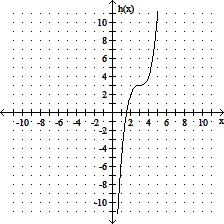
C. 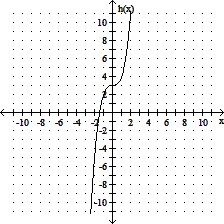
D. 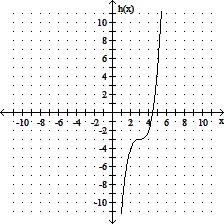
Solve the problem.An object's acceleration at time t is given by a = 14t, and its initial velocity is 5. Find the object's velocity as a function of time.
A. v = 5t2 + 14 B. v = 7t2 + 5 C. v = 14t2 + 5 D. v = 7t2 + 5t
Compute.-11 + 22
A. -33 B. 11 C. 33 D. -11
Solve.A painting was sold in 1985 for $ 2 million. The painting was then resold in 1996 for $ 6 million. Assume that the painting's value increases exponentially. Find the exponential growth rate k, and determine the exponential growth function, assuming V0 = 2. (Round decimals to three places.)
A. k = 0.1; V(t) = 2e0.1, where V(t) is in millions and t is the number of years after 1985. B. k = 0.1; V(t) = 2e0.1t, where V(t) is in millions and t is the number of years after 1985. C. k = 0.1; V(t) = 2e0.1t, where V(t) is in millions and t is the number of years after 1997. D. k = 0.092; V(t) = 2e0.092t, where V(t) is in millions and t is the number of years after 1985.