Find an equation for the hyperbola described.Vertices at (±8, 0); foci at (±10, 0)
A.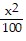 
- 
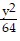= 1
B. 
- 
= 1
C. 
- 
= 1
D. 
- 
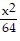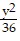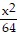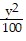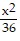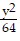= 1
Answer: B
You might also like to view...
Graph the parabola or ellipse. Include the directrix that corresponds to the focus at the origin.r =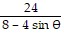 
A.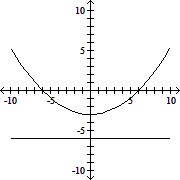 
B. 
C. 
D.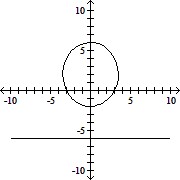 
Solve the problem. Round your result to an appropriate number of significant digits.A lake lies between A and C, and lines AB and DE run north-south. If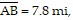 
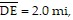and 
how far is it from A to C?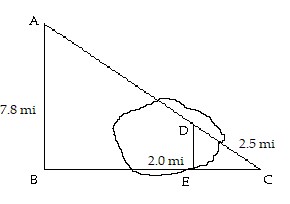
A. 9.8 mi B. 7.3 mi C. 10 mi D. 6.2 mi
Find the perimeter of the figure.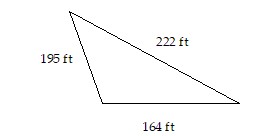
A. The perimeter is 581 feet. B. The perimeter is 417 feet. C. The perimeter is 571 feet. D. The perimeter is 36,825 feet.
Find the center, transverse axis, vertices, foci, and the equations of the asymptotes of the hyperbola.(x + 1)2 - 9(y - 2)2 = 9
A. center: (-1, 2)
transverse axis: x = -1
vertices: (-1, -1) and (-1, 5),
foci: (-1, 2 -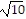 
) and (-1, 2 + 
),
asymptotes: y + 2 = - 3(x - 1) and y + 2 = 3(x - 1)
B. center: (2, -1)
transverse axis: y = 2
vertices: (-1, -1) and (5, -1)
foci: (2 -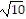 
, -1) and (2 + 
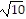, -1)
asymptotes: y + 1 = -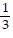 
(x - 2) and y + 1 = 
(x - 2)
C. center: (-1, 2)
transverse axis: y = 2
vertices: (-4, 2) and (2, 2)
foci: (-1 -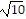 
, 2) and (-1 + 
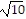, 2)
asymptotes: y - 2 = - 
(x + 1) and y - 2 =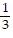 
(x + 1)
D. center: (-1, 2)
transverse axis: y = 2
vertices: (-2, 2) and (0, 2)
foci: (-1 - 
, 2) and (-1 + 
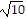, 2)
asymptotes: y - 2 = - 3(x + 1) and y - 2 = 3(x + 1)