Solve the problem.Tides go up and down in a 12.4-hour period. The average depth of a certain river is 10 m and ranges from 5 to 15 m. The variation can be approximated by a sine curve. Write an equation that gives the approximate variation y, if x is the number of hours after midnight and high tide occurs at 5:00 am.
A. y = 5 sin  + 10
+ 10
B. y = 10 sin 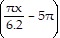 + 5
+ 5
C. y = 10 sin  + 5
+ 5
D. y = 5 sin  + 10
+ 10
Answer: A
You might also like to view...
Determine whether the statement is true or false. 22 ? {x|x ? N and 15 < x ? 25}
A. True B. False
Provide an appropriate response.Determine whether the algebraic expression 4x5 + 3x2 is a polynomial (Yes or No). If it is a polynomial, state the degree and then state if it is a monomial, binomial, or trinomial.
A. yes; degree 2; binomial B. yes; degree 5; binomial C. yes; degree 5; trinomial D. no
Solve the problem.Two angles are supplementary, and one is 5° more than six times the other. Find the larger angle.
A. 70° B. 25° C. 155° D. 110°
Solve the problem.A ship travels 64 km on a bearing of 14°, and then travels on a bearing of 104° for 139 km. To the nearest kilometer, find the distance from the start to the end of the trip.
A. 15 km B. 153 km C. 203 km D. 62 km