Find the nth, or general, term.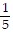
, 
, 
, . . .
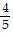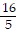A.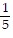 
+ 4(n - 1)
B.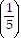 
n-1+ 
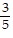
C.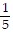 
(4)n-1
D.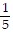 
+ 
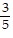(n - 1)
Answer: C
You might also like to view...
Solve the problem.A model that describes the free fall of an object in a gravitational field subject to air resistance uses the equation src="https://sciemce.com/media/4/ppg__tttt0613190828__f1q57g5.jpg" alt="" style="vertical-align: -4.0px;" /> For what initial values 
where v(t) is the velocity of the object, for 
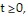
is the acceleration due to gravity, and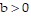 
is a constant that involve the mass of the object and the air resistance. Let 
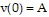are solutions increasing? decreasing? What is the equilibrium solution?
A. increasing for A > 24.5 and decreasing for A < 24.5; v(t) = 24.5
B. increasing for A > 24.5 and decreasing for A < 24.5; v(t) = 0
C. increasing for A < 24.5 and decreasing for A > 24.5; v(t) = 24.5
D. increasing for A < 24.5 and decreasing for A > 24.5; v(t) = 0
Solve the equation.
= 
A. {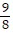
, 
}
B. {-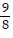 
, - 
}
C. {
, - 
}
D. ?
Solve the problem.Use Ohm's Law, I =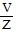 
, to find the current I, given voltage 
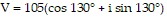and impedance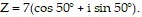 
A. 15(cos 80° + i sin 80°) B. 1575(cos 180° + i sin 180°) C. 15(cos 26.0° + i sin 26.0°) D. 98(cos 80° + i sin 80°)
Complete the table for the function and find the indicated limit.
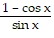
A. -0.0300, -0.0200, -0.0100, 0.0100, 0.0200, 0.0300 limit = 0.1 B. -0.0300, -0.0200, -0.0100, 0.0100, 0.0200, 0.0300 limit = 1 C. -0.0300, -0.0200, -0.0100, 0.0100, 0.0200, 0.0300 limit = -1 D. -0.0150, -0.0100, -0.0050, 0.0050, 0.0100, 0.0150 limit = 0