Convert the given equation to parametric equations. Answers may vary.y = 6 - x2
A. x = t, y = (6 - t)2
B. y = t, x = 6 - t2
C. x = t, y = 6 - t
D. x = t, y = 6 - t2
Answer: D
You might also like to view...
Solve the problem.During one year 13 new employees began work at Daniel's Manufacturing Company and 14 employees left. At the beginning of the year there were 398 employees. What was the number of employees at the end of the year?
A. 397 employees B. 371 employees C. 425 employees D. 411 employees
Find the equation for the curve in its final position.The graph y = sin (x) is shifted a distance of ?/12 to the left, reflected in the x-axis, translated 7 units downward, then stretched by a factor of 4.
A. y = -4 sin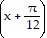 
- 28
B. y = -4 sin 
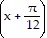- 7
C. y = -4 sin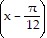 
- 28
D. y = -4 sin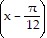 
+ 28
Change the equation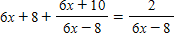 
to quadratic form and solve it by any method. Round your answer to two decimal places.
?
A. 1.33, -2.33 B. 1.17, -2.50 C. 2.50, -2.33 D. 2.50, -1.17 E. -1.33, 1.17
Simplify.(-r4s)2( -r2s2)5
A. -r48s34 B. r18s12 C. -r-2s12 D. -r18s12