Solve.A rectangular box with volume 468 cubic feet is built with a square base and top. The cost is $1.50 per square foot for the top and the bottom and $2.00 per square foot for the sides. Let x represent the length of a side of the base in feet. Express the cost of the box as a function of x and then graph this function. From the graph find the value of x, to the nearest hundredth of a foot, which will minimize the cost of the box.
A. 8.55 feet
B. 8.63 feet
C. 8.44 feet
D. 7.92 feet
Answer: A
Mathematics
You might also like to view...
Solve graphically. Round solutions to three decimal places, where appropriate.x2 - 7x + 9 = 0
A. 1.747, 5.353 B. 0.017, 0.053 C. 1.697, 5.303 D. 3.394, 10.606
Mathematics
Add.(2r2s2 + 3r2s - 7rs) + (7r2s2 - 2r2s + 7rs - 4)
A. 9r2s2 + r2s - 4 B. 9r2s2 + 5r2s - 14rs - 4 C. 9r2s2 + 5r2s + 14rs + 4 D. 9r2s2 + r2s - 14rs - 4
Mathematics
Use the properties of logarithms to write the expression as the logarithm of a single expression.ln x2 - 4 ln 
A. ln x3/2 B. 4 C. 0 D. ln x1/2
Mathematics
Solve using Cramer's rule.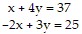
A. (-1, 10) B. (0, 10) C. (1, 9) D. No solution
Mathematics