Use mathematical induction to prove the following.1 ? 3 + 2 ? 4 + 3 ? 5 + . . . + n(n + 2) =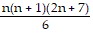 
What will be an ideal response?
Answers may vary. One possibility:
Sn: 1 ? 3 + 2 ? 4 + 3 ? 5 + . . . + n(n + 2) =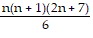 
S1: 1 ? 3 =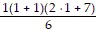 
Sk: 1 ? 3 + 2 ? 4 + 3 ? 5 + . . . + k(k + 2) =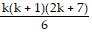 
Sk+1: 1 ? 3 + 2 ? 4 + 3 ? 5 + . . . + k(k + 2) + (k + 1)(k + 3) =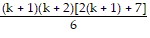 
1. Basis step: Since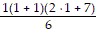 
= 
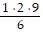= 1 ? 3, S1 is true.
2. Induction step: Let k be any natural number. Assume Sk. Deduce Sk+1.
1 ? 3 + 2 ? 4 + 3 ? 5 + . . . + k(k + 2) =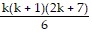 
1 ? 3 + 2 ? 4 + 3 ? 5 + . . . + k(k + 2) + (k + 1)(k + 3) =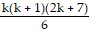 
+ (k + 1)(k + 3)
= 
+ 
= 
+ 
= 
= 
= 
= 
= 
.
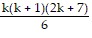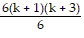
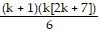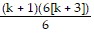
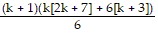
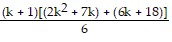
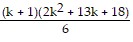
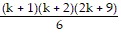
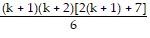You might also like to view...
Solve the problem.The shape of a parabolic flashlight reflector can be described by the equation x = 8y2. Where should the light bulb be placed?
A.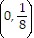 
B. 
C. (32, 0)
D.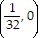 
A point on the terminal side of angle ? is given. Find the exact value of the indicated trigonometric function of ?.(-9, -4) Find cot ?.
A. -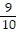 
B. -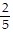 
C.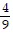 
D.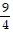 
Simplify the exponential expression.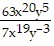
A. 9xy8 B. 9x39y8 C. 63xy8 D. 9xy2
Solve the system of equations by elimination.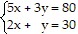
A. x = 0, y = 0; (0, 0) B. x = 10, y = 0; (10, 0) C. x = 0, y = 10; (0, 10) D. x = 10, y = 10; (10, 10)