A manufacturer of tennis rackets finds that the total cost  (in dollars) of manufacturing
(in dollars) of manufacturing 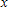 rackets/day is given by
rackets/day is given by 
varid="variable_id_field" variablename="impvar_d5d1460973ce46d18ae5f0bcd" />. Each racket can be sold at a price of 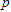


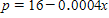
?
If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
?
__________ rackets/day
Fill in the blank(s) with the appropriate word(s).
14,000
You might also like to view...
Solve the system using the inverse of the coefficient matrix of the equivalent matrix equation.-5x + 3y = 83x - 6y = -30
A. (6, 2) B. (-2, -6) C. (2, 6) D. (-6, -2)
Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C.F = (x2 + y2)i + (x - y)j; C is the rectangle with vertices at (0, 0), (3, 0), (3, 7), and (0, 7)
A. 168 B. -126 C. 126 D. 0
Solve the system of equations by use of determinants. y + z = 93x- z = 2 2x + y + 3z = 7
A. x = 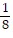 , y =
, y = 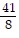 , z = -
, z = - 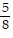
B. x = 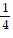 , y =
, y = 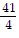 , z = -
, z = - 
C. x =  , y =
, y = 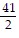 , z = -
, z = - 
D. x = -  , y = -
, y = -  , z =
, z = 
Solve the problem.A power plant is located on a river that is 700 feet wide. To lay a new cable from the plant to a location in a city 1 mile downstream on the opposite side costs $175 per foot across the river and $150 per foot along the land. Suppose that the cable goes from the plant to a point Q on the opposite side that is x feet from the point P directly opposite the plant. Write a function C(x) that gives the cost of laying the cable in terms of the 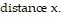
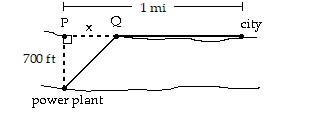
A. C(x) = 150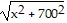 + 175(5280 - x)
+ 175(5280 - x)
B. C(x) = 175(700 - x) + 150(1 - x)
C. C(x) = 175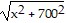 + 150(5280 - x)
+ 150(5280 - x)
D. C(x) = 175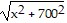 + 150(1 - x)
+ 150(1 - x)