Convert the angle from degrees to radians. Express the answer as a multiple of ?.-650°
A. - 
B. - 
C. - 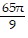
D. - 
Answer: D
You might also like to view...
Provide an appropriate response.Divide and reduce answer to lowest terms converting improper fractions to whole or mixed numbers: 6 ÷ 3
A. 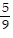
B. 
C. 20
D. 
Solve the problem.A company that produces appliances has found that revenue from the sales of the appliances is $50 per appliance, less sales costs of $250. Production costs are $400, plus $40 per appliance. Profit (P) is given by revenue (R) less cost (C), so the company must find the production level x that makes P > 0, that is, R - C > 0.(a) Write an expression for revenue, R, letting x represent the production level (number of appliances to be produced.)(b) Write an expression for production costs C in terms of x.(c) Write an expression for profit P, and then solve the inequality P > 0.(d) Describe the solution in terms of the problem.
A. (a) R = 50x - 250;
(b) C = 400 + 40x;
(c) P = (50x - 250) - (400 + 40x) = 5x - 650; 5x > 650; x > 130
(d) To make a profit, more than 130 appliances must be produced and sold.
B. (a) R = 50x + 250;
(b) C = 400 - 40x;
(c) P = (50x + 250) - (400 - 40x) = 10x - 150; 10x > 150; x > 15
(d) To make a profit, more than 15 appliances must be produced and sold.
C. (a) R = 50x - 250;
(b) C = 400 +
Simplify the expression. Assume that all variables are positive when they appear.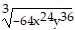
A. -4x12y18 B. 16x8y12 C. -4x8y12 D. 4x8y12
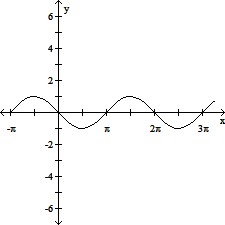
Use transformations to graph the function.y = sin (?x)
A. 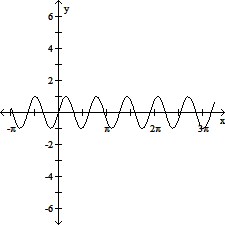
B. 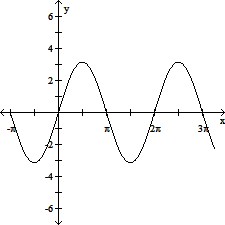
C. 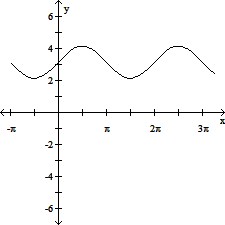
D.