Use mathematical induction to prove the statement is true for all positive integers n.n(n + 6) < (n + 3)2
What will be an ideal response?
Answers may vary. Possible answer:
First, we show the statement is true when n = 1.
For n = 1, 1(1 + 6) = 7 < 16 = (1 + 3)2
So P1 is true and the first condition for the principle of induction is satisfied.
Next, we assume the statement holds for some unspecified natural number k. That is,
Pk: k(k + 6) < (k + 3)2 is assumed true.
On the basis of the assumption that Pk is true, we need to show that Pk+1 is true.
Pk+1: (k + 1)((k + 1) + 6) < ((k + 1) + 3)2
(k + 1)((k + 1) + 6) = (k + 1)(k + 7) = k2 + 8k + 7 = k(k + 6) + (2k + 7)
Since Pk is assumed true, 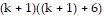 =
= 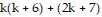 <
< 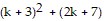 =
= 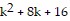 =
= 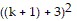
So Pk+1 is true if Pk is assumed true. Therefore, by the principle of mathematical induction, 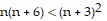 for all natural numbers n.
for all natural numbers n.
You might also like to view...
Provide an appropriate response.If the sides of a triangle measure 12 m, 12 m, and 1,200 cm, what kind of triangle is it?
A. isosceles triangle B. equilateral triangle C. right triangle D. scalene triangle
Sketch the graph of the function and its inverse on the same coordinate axes.y = x3 + 1
A. 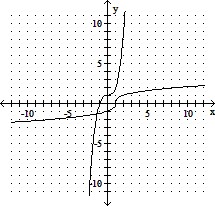
B. 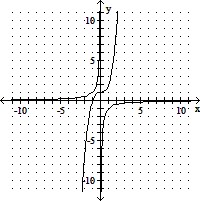
C. 
D. 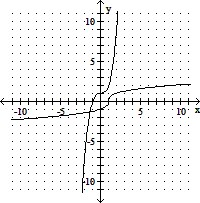
Graph.(x - 2)2 + (y - 3)2 = 9
A. 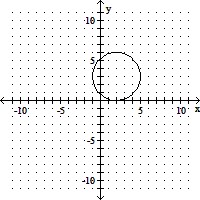
B. 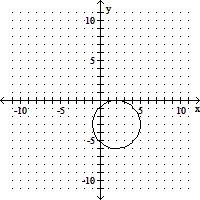
C. 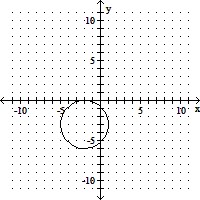
D. 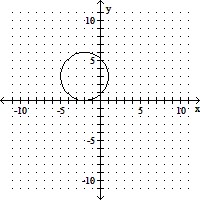
Solve.Andy wants to buy a refrigerator for $699, a stove for $459, and a dishwasher for $349. Round each cost to the nearest hundred to estimate the total cost.
A. $1400 B. $1600 C. $1300 D. $1500