Soundex produces two models of clock radios. Model A requires 15 min of work on assembly line I and 10 min of work on assembly line II. Model B requires 12 min of work on assembly line I and 20 min of work on assembly line II. At most 21 hr of assembly time on line I and 20 hr of assembly time on line II are available each day. Soundex anticipates a profit of $12 on model A and $10 on model B. Because of previous overproduction, management decides to limit the production of model A clock radios to no more than 80/day
To maximize Soundex's profit, how many clock radios of each model should be produced each day? Find the range of values that the contribution to the profit of a model A clock radio can assume without changing the optimal solution. Identify the binding and nonbinding constraints.


You might also like to view...
L'Hopital's rule does not help with the given limit. Find the limit some other way.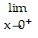
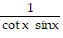
A. -1 B. 0 C. ? D. 1
Find an equation of the line passing through the two points. Write the equation in standard form.(-5, -9) and (0, -7)
A. -2x - 5y = 35 B. 2x - 5y = 35 C. 4x + 7y = -49 D. -4x - 7y = -49
Use the quadratic formula to solve the quadratic equation.5x2 = 3x - 3
A. - 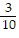 ±
± 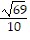
B. no real solution
C. 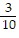 ±
± 
D. all real numbers
For the given simplex tableau, determine which variable should be brought into the solution and which row to use as a pivot. x1 x2 x3 x4 M
A. x1, row 2 B. x2, row 1 C. x1, row 1 D. x2, row 2