Use Euler's method to calculate the first three approximations to the given initial value problem for the specified increment size. Round your results to four decimal places.y' = 1 + 
, y(4) = -1, dx = 0.5
A. y1 = -1.2500, y2 = -0.3889, y3 = 1.1444
B. y1 = -1.2500, y2 = -0.2917, y3 = 0.5722
C. y1 = -0.9375, y2 = -0.2333, y3 = 0.3433
D. y1 = -0.6250, y2 = -0.1944, y3 = 0.2861
Answer: D
You might also like to view...
The following table shows the running speed R, in feet per second, of animals of length L, in inches. If one animal is 5 inches longer than another, then based on the regression equation, how would their running speeds compare? L 3.5 6.3 9.4 9.8 R 8.21 15.72 24.05 24.95? ?
A. The longer animal would run 2.67 times faster than the shorter animal. B. The longer animal would run 13.35 times faster than the shorter animal. C. The longer animal would run 13.35 feet per second faster than the shorter animal. D. The longer animal would run 2.67 feet per second faster than the shorter animal.
Graph the sinusoidal function using key points.y = 4 sin(?x)
A. 
B. 
C. 
D. 
Which compound proposition is true?
 figure 1.png)
Solve the problem involving a radical equation. Round to the nearest hundredth if necessary.If a car traveling on asphalt skids to a stop, with all four of its wheels braking evenly, the car's original speed is related to the average length of the skid marks by s =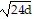 
, where s is the speed in miles per 
d is the average length of the skid marks in feet. What is the distance required to skid to a stop for a car that is traveling 60 miles per hour.
A. 37.95 ft B. 15 ft C. 150 ft D. 86,400 ft