Use the Principle of Mathematical Induction to show that the statement is true for all natural numbers n.
is divisible by 2
What will be an ideal response?
First, we show that the statement is true when n = 1.
For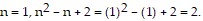 
This is a true statement and Condition I is satisfied.
Next, we assume the statement holds for some k. That is,
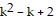is divisible by 2 is true for some positive integer k.
We need to show that the statement holds for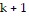 
. That is, we need to show that
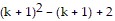is divisible by 2.
So we assume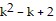 
is divisible by 2 and look at the expression for n = k + 1.
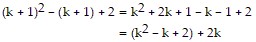
Since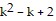 
is divisible by 2, then 
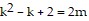for some integer m. Hence,
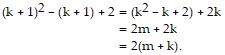
Condition II is satisfied. As a result, the statement is true for all natural numbers n.
You might also like to view...
Use the appropriate formula to find the indicated figurate number.the 9th triangular number
A. T9 = 36 B. T9 = 40.5 C. T9 = 45 D. T9 = 90
Determine the values of x for which the function, as represented by the graph, is continuous. If the function is not continuous, determine the reason.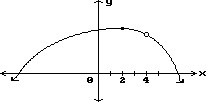
A. Not continuous at x = 4; small change B. Not continuous at x = 2, x = 4; function not defined C. Not continuous at x = 2, x = 4; small change D. Not continuous at x = 4; function not defined
Find the exact value. If any are not defined, write undefined.sin 450°
A. 0
B. 1
C. Undefined
D.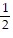 
Solve the following circle graph problems.If rent is represented by 54° on a circle graph showing all expenses, and the cost of rent is $765, how much are the total expenses?
A. $6,120 B. $6,375 C. $4,590 D. $5,100