Use Bayes' rule to find the indicated probability.The incidence of a certain disease on the island of Tukow is 4%. A new test has been developed to diagnose the disease. Using this test, 91% of those who have the disease test positive while 4% of those who do not have the disease test positive (false positive). If a person tests positive, what is the probability that he or she actually has the disease?
A. 0.438
B. 0.487
C. 0.91
D. 0.856
Answer: B
You might also like to view...
Provide an appropriate response.Which, if any, of the following statements are true?A: If a number is divisible by 9, it must be divisible by 3. B: If a number is divisible by 3, it must be divisible by 9.
A. A false, B true B. A true, B false C. A false, B false D. A true, B true
Add.(2x8 - 9x3 + 2x2 + 7) + (4x7 + 5x3 - 9x)
A. 2x8 + 4x7 + 4x3 + 2x2 - 9x + 7 B. 6x8 - 14x3 + 2x2 - 9x + 7 C. 6x8 - 4x3 + 2x2 - 9x + 7 D. 2x8 + 4x7 - 4x3 + 2x2 - 9x + 7
Multiply, then simplify the product. If variables are present, assume they are positive.(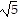
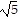+ 1)(
- 1)
A. 4 + 2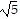
B. 6
C. 4 - 2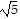
D. 4
Find the unknown value in the percent proportion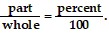 
Round to the nearest tenth, if necessary.part = 4, whole = 15
A. percent = 26.7% B. percent = 375% C. percent = 2.7% D. percent = 13.4%