Solve the problem.The columns of I3 =  are e1 =
are e1 = 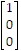 , e2 =
, e2 = 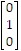 , e3 =
, e3 = 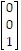 .Suppose that T is a linear transformation from ?3 into ?2 such that T( e1) =
.Suppose that T is a linear transformation from ?3 into ?2 such that T( e1) = 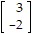 , T( e2) =
, T( e2) = 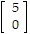
style="vertical-align: -15.0px;" /> , and T( e3) = 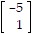 .Find a formula for the image of an arbitrary x =
.Find a formula for the image of an arbitrary x = 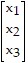 in ?3.
in ?3.
A.
T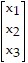 =
= 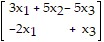
B.
T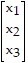 =
= 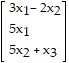
C.
T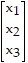 =
= 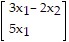
D.
T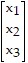 =
= 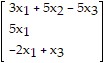
Answer: A
Mathematics
You might also like to view...
Find all local extreme values of the given function and identify each as a local maximum, local minimum, or saddle point.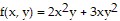
A. f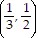 =
= 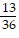 , local minimum
, local minimum
B. 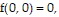 saddle point
saddle point
C. f(6, 6) = 1,080, local maximum
D. f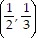 =
= 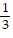 , local minimum
, local minimum
Mathematics
Factor by grouping.18dx - 9dy - 12hx + 6hy
A. 3(3d - 2h)(2x + y) B. 3(3d + 2h)(2x - y) C. 3(3d - 2h)(2x - y) D. 3(3d + 2h)(2x + y)
Mathematics
Identify the property that allows you to conclude that the triangles are congruent. Or, if such a conclusion cannot be made, answer "None."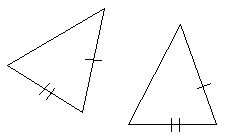
A. None B. SAS C. ASA D. SSS
Mathematics
Solve the equation.u2 + 16u + 47 = 0
A. -16 + 
B. 8 + 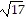
C. -8 -  , -8 +
, -8 + 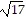
D. 8 -  , 8 +
, 8 + 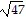
Mathematics