Solve the problem.A product of two oscillations with different frequencies such as f(t) = sin (10t) sin(t)is important in acoustics. The result is an oscillation with "oscillating amplitude." the product f(t) of the two oscillations as a sum of two cosines and call it g(t).
the product f(t) of the two oscillations as a sum of two cosines and call it g(t). a graphing utility, graph the function g(t) on the interval 0 ? t ? 2?.
a graphing utility, graph the function g(t) on the interval 0 ? t ? 2?. the same system as your graph, graph y = sin t and y = -sin t.
the same system as your graph, graph y = sin t and y = -sin t.
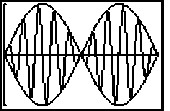
src="https://sciemce.com/media/4/ppg__qas0526191658__f1q86g4.jpg" alt="" style="vertical-align: -4.0px;" /> last two functions constitute an "envelope" for the function g(t). For certain values of t, the two cosine functions in g(t) cancel each other out and near-silence occurs; between these values, the two functions combine in varying degrees. The phenomenon is known (and heard) as "beats." For what values of t do the functions cancel each other?
What will be an ideal response?
(i) g(t) = 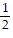 cos(9t) -
cos(9t) - 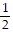 cos(11t)
cos(11t)
(ii), (iii)
(iv) t = 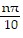 , n any integer
, n any integer
Mathematics
src="https://sciemce.com/media/4/ppg__qas0526191658__f1q86g4.jpg" alt="" style="vertical-align: -4.0px;" /> last two functions constitute an "envelope" for the function g(t). For certain values of t, the two cosine functions in g(t) cancel each other out and near-silence occurs; between these values, the two functions combine in varying degrees. The phenomenon is known (and heard) as "beats." For what values of t do the functions cancel each other?
What will be an ideal response?
| (i) | g(t) = 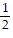 cos(9t) - cos(9t) - 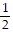 cos(11t) cos(11t) |

(iv) t =
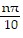 , n any integer
, n any integerYou might also like to view...
Find the indicated probability. Round your answer to 6 decimal places when necessary.In January in a certain city the unconditional probability of rain on any given day of the month is 0.400. But the probability of rain on a day that follows a rainy day is 0.600 and the probability of rain on a day following a nonrainy day is 0.250. Find the probability that January 1st and January 2nd are rainy and that January 3rd and 4th are not rainy given that December 31st was clear all day.
A. 0.072 B. 0.024 C. 0.045 D. 0.038
Solve the problem.Rewrite the integral 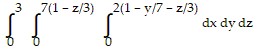 in the order
in the order 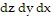 .
.
A. 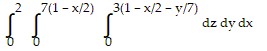
B. 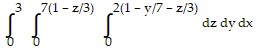
C. 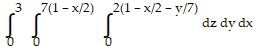
D. 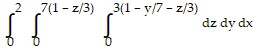
Find the measure of the indicated angle.Two angles of a triangle are 43° and 106°. Find the third angle.
A. 31° B. 149° C. 59° D. 211°
Use Gauss-Jordan elimination to solve the linear system and determine whether the system has a unique solution, no solution, or infinitely many solutions. If the system has infinitely many solutions, describe the solution as an ordered triple involving variable z.4x - y + 3z=12x + 4y + 6z=-325x + 3y + 9z=20
A. (-8, -7, 9) B. (2, -7, -1) C. no solution D. (8, -7, -2)