Solve the problem.A formula for calculating the distance, d, one can see from an airplane to the horizon on a clear day is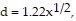 
where x is the altitude of the plane in feet and d is given in miles. How far can one see in a plane flying at 30,000 feet? Round your answer to the nearest tenth mile, if necessary.
A. 18,300 mi
B. 191.3 mi
C. 1830 mi
D. 211.3 mi
Answer: D
You might also like to view...
Use the given information to find the unknown length represented by the variable x.A rectangle with a perimeter of 256 feet
x
A. 105 ft B. 2415 ft C. 151 ft D. 128 ft
For the equation, create a table, -3 ? x ? 3, and list points on the graph.2x + 3y = 6
A.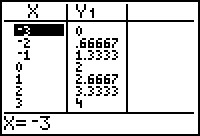 
(-3, 0), (-2, 0.67), (-1, 1.33), (0, 2),
(1, 2.67), (2, 3.33), (3, 4)
B.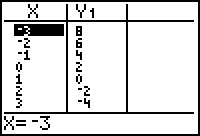 
(-3, 8), (-2, 6), (-1, 4), (0, 2), (1, 0),
(2, -2), (3, -4)
C.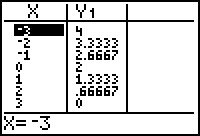 
(-3, 4), (-2, 3.33), (-1, 2.67), (0, 2),
(1, 1.33), (2, 0.67), (3, 0)
D.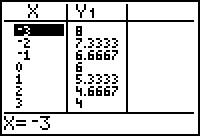 
(-3, 8), (-2, 7.33), (-1, 6.67), (0, 6), (1, 5.33),
(2, 4.67), (3, 4)
Identify whether the equation is a linear equation in two variables. Answer "is" or "is not."y = 8x2
A. is B. is not
Determine whether the matrix is an absorbing stochastic matrix.
A. Yes B. No