Provide an appropriate response.Plot the functions u(x) = 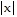 , l(x) = -
, l(x) = -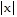 , and f(x) = x cos (1/x2). Then use these graphs along with the Squeeze Theorem to prove that
, and f(x) = x cos (1/x2). Then use these graphs along with the Squeeze Theorem to prove that 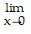 f(x) = 0.
f(x) = 0.
What will be an ideal response?
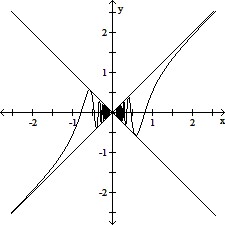
From the graph, it can be seen that the graph of f(x) = x cos (1/x2) is between the graphs of l(x) = -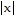 and u(x) =
and u(x) = 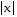 . Also
. Also 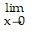
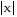 = 0 and
= 0 and 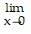 (-
(- ) = 0. Since the graph of f(x) = x cos (1/x2) is squeezed between the graphs of
) = 0. Since the graph of f(x) = x cos (1/x2) is squeezed between the graphs of 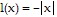 and
and 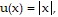 both of which go to 0 as x?0, by the Squeeze Theorem we can conclude that
both of which go to 0 as x?0, by the Squeeze Theorem we can conclude that 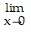 f(x) = 0 .
f(x) = 0 .
You might also like to view...
Find the average value of the function f over the given region.f(x, y) = 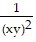 ; R = {(x, y): 1 ? x ? 5, 1 ? y ? 5}
; R = {(x, y): 1 ? x ? 5, 1 ? y ? 5}
A. 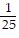
B. 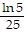
C. 
D. 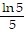
Find the equation of the line passing through the indicated two points. Write the equation in slope-intercept form.(-3, -2) and (-5, -8)
A. y = -6x - 20 B. y = -2x - 8 C. y = 3x + 7 D. x = -3
Convert to radian measure. Round to two decimal places.78.2°
A. 1.36 B. 1.37 C. 1.33 D. 1.32
Solve.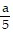 -
- 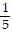 = -6
= -6
A. 29 B. -29 C. 31 D. -31