Solve the problem.Suppose that an insect population density, in thousands, during year n can be modeled by the recursively defined sequence: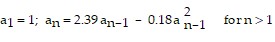 
.Use technology to graph the sequence for n = 1 , 2 , 3 , ........., 20 . Describe what happens to the population density function.
A. The insect population stabilizes near 4.52 thousand.
B. The insect population stabilizes near 7.72 thousand.
C. The insect population stabilizes near 7.18 thousand.
D. The insect population increases every year.
Answer: B
Mathematics
You might also like to view...
Round the number so that there is only one nonzero digit.769
A. 790 B. 900 C. 700 D. 800
Mathematics
Factor completely.x2 - 2xy - 35y2
A. (x - 7y)(x + 5y) B. (x - 7y)(x + y) C. (x + 7y)(x - 5y) D. (x - y)(x + 5y)
Mathematics
Solve by the substitution method.8x + 17 = 7y5x - 3y = -12
A. (7, -12) B. (-1, -3) C. (-4, 0) D. (-3, -1)
Mathematics
Theresa made 37 of 41 free throws at basketball practice. Which percent did she make? Round your answer to tenth percent.
a. 91.9 b. 85.2 c. 90.2 d. 87.1
Mathematics