Given 
(a) Find the intervals on which f is increasing or decreasing.
(b) Find the relative maxima and relative minima of f.
a. (a) Increasing on (?6, 6), decreasing on (??, ?6) and (6, ?)
(b) Rel. max. f(6) = 12,
rel. min. f(?6) = ?12
b. (a) Increasing on (?6, 0) and (0,6) decreasing on (??, ?6) and (6, ?)
(b) Rel. max. f(6) = 12,
rel. min. f(?6) = ?12
c. (a) Increasing on (??, ?6) and (6, ?), decreasing on (?6, 0) and (0,6)
(b) Rel. max. f(?6) = ?12,
rel. min. f(6) = 12
d. (a) Increasing on (??, ?6) and (6, ?), decreasing on (?6, 6)
(b) Rel. max. f(?6) = ?12,
rel. min. f(6) = 12
c. (a) Increasing on (??, ?6) and (6, ?), decreasing on (?6, 0) and (0,6)
(b) Rel. max. f(?6) = ?12,
rel. min. f(6) = 12
You might also like to view...
Evaluate the determinant.
A. 0 B. 21x C. 21x - 3 D. 3 - 21x
Use logarithmic differentiation to find the derivative of y.y =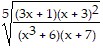 
A.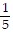 
(ln(3x + 1) + 2ln(x + 3) - ln(x3 + 6) - ln(x + 7))
B. 5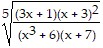
C.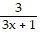 
+ 
- 
- 
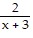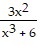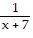
D. 
Solve the problem.The following graph shows weekend gross revenue for a summer blockbuster film.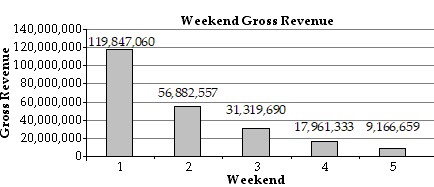 
Find the total revenue the film earned over weekends 3 and 4.
A. $58,447,682 B. $49,281,023 C. $13,358,357 D. $31,319,690
Identify the degree of each term and the degree of the polynomial.6x5 - 9x2 + 6 - 2x3
A. 5, 3, 2, 0; 5 B. 5, -2, 1, -3; 5 C. 6, -9, 6, -2; 6 D. 5, 2, 0, 3; 5