Solve the problem.A furniture manufacturer makes TV tables and bookcases in the same workshop. Each item brings in a profit of $18. Each bookcase requires 2 hours of labor 3 units of teak wood. Each TV table requires 6 hours of labor and 1 unit of teak wood. Resources in the workshop are restricted to 6 units of teak wood a day and 12 hours of labor per day. The initial and final tableaux are given below with x = the number of TV tables and y = the number of bookcases produced each day.?
 ?
?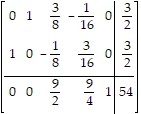
style="vertical-align: -49.0px;" />(initial)(final)(a)What is the optimal production schedule and maximum daily profit?(b) If the amount of available teak wood can be increased to 10 units per day, how does the production schedule change? How do maximum profits change?(c) If the amount of teak changes by h units in a day, how would the optimal production schedule and maximum profit change?(d) What restrictions should be placed on the size of h to make the analysis in (c) valid?
What will be an ideal response?
| (a) | x = 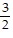 , y = , y = 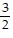 , M = $54 , M = $54 |
| (c) | x = 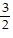 - - 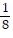 h, y = h, y = 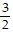 + + 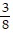 h, and M = 54 + h, and M = 54 + 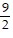 h. h. |
You might also like to view...
Find  .e2x = sin (x + 2y)
.e2x = sin (x + 2y)
A. 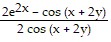
B. 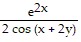
C. 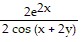 -1
-1
D. ln sin (x + 2y)
Find the point at which the line given by the parametric equations below intersects the plane.
2x+4y-3z=-48, x=10+7t, y=-10, z=7t
 multiple choice.png)
Solve the problem.A pest control company sprays insecticide around the perimeter of a 340 ft by 420 ft building. If the spray costs $0.13 per foot, how much did the job cost to the nearest dollar?
A. $198 B. $99 C. $18,564 D. $1547
Write the number in scientific notation.819,000
A. 8.2 × 10-5 B. 8.2 × 105 C. 8.2 × 104 D. 8.2 × 10-4