A student has the following attendance pattern. If he is present in class one day, the probability he will be present the next day is 0.5.If he is absent from class one day, the probability he will be present the next day is 0.4.(a) Write this as a transition matrix using present and absent as the state.(b) If he attends class the first day, find the probability he will be present the second day.(c) If he attends class the first day, find the probability he will be present the third day.(d) Find percent of time the student will be present in the long run.
What will be an ideal response?
(a)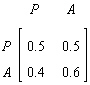
(b) 0.5
(c) 0.45
(d)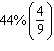 
Mathematics
You might also like to view...
Evaluate the integral.
A. -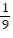 
cot33x + 
cot 3x + x + C
B. -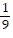 
cot33x + 
cot2 3x + x + C
C. - 
cot33x + cot 3x + x + C
D. -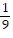 
cot33x + 
cot 3x + C
Mathematics
Solve the problem.Dave puts a collection of 15 books on a bookshelf in a random order. Among the books are 2 fiction and 13 nonfiction books. What is the probability that the 2 fiction books will be together on the left side of the shelf and the 13 nonfiction all together on the right side of the shelf?
A. 0.01809 B. 0.01619 C. 0.00952 D. 0.01333
Mathematics
Evaluate the expression according to the order of operations.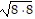
- 4
A. 4 B. 60 C. 68 D. 12
Mathematics
(6 + j3)(2 + j2) =
a. 12 + j6 b. 12 + j18 c. 6 + j6 d. 6 + j18 e. 6 + j12
Mathematics