Solve the problem.At a ticket booth, customers arrive randomly at a rate of x per hour. The average line length is 
where 
To keep the time waiting in line reasonable, it is decided that the average line length should not exceed 10 customers. Solve the inequality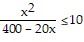 
to determine the rates x per hour at which customers can arrive before a second attendant is needed.
A. 0 ? x ? 19
B. 0 ? x ? 17
C. 0 ? x ? 18
D. 0 ? x ? 20
Answer: C
Mathematics
You might also like to view...
The position vector of a particle is r(t). Find the requested vector.The acceleration at t = 
for r(t) = (4 sin 2t)i - (5 cos 2t)j + (3 csc 2t)k
A. a
= -16i + 12k
B. a
= 20j + 12k
C. a
= 16i + 12k
D. a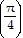
= -16i - 12k
Mathematics
Graph the function by plotting points.f(x) =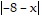 
+ 1
A.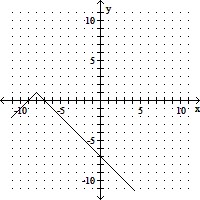 
B.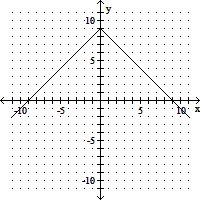 
C.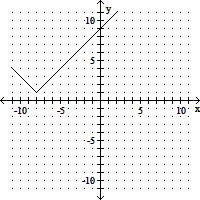 
D.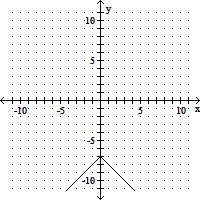 
Mathematics
Provide an appropriate response.Show that the nth triangular number is 
.
What will be an ideal response?
Mathematics
Simplify.240 ÷ 5 - 4
A. 231 B. 240 C. 44 D. 239
Mathematics