Answer each question appropriately.If differentiable functions y = F(x) and y = G(x) both solve the initial value problem 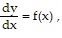
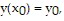 on an interval I, must
on an interval I, must 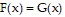 for every x in I? Justify the answer.
for every x in I? Justify the answer.
A. F(x) = G(x) for every x in I because integrating f(x) results in one unique function.
B. F(x) = G(x) for every x in I because when given an initial condition, we can find the integration constant when integrating f(x). Therefore, the particular solution to the initial value problem is unique.
C. F(x) and G(x) are not unique. There are infinitely many functions that solve the initial value problem. When solving the problem there is an integration constant C that can be any value. F(x) and G(x) could each have a different constant term.
D. There is not enough information given to determine if F(x) = G(x).
Answer: B
You might also like to view...
Solve the problem.In a clinical study, 19 of the 380 subjects receiving a migraine medication developed side effects. What percentage developed side effects?
A. 15% B. 7% C. 5% D. 4%
Construct the following
Use properties of logarithms to condense the logarithmic expression. Write the expression as a single logarithm whose coefficient is 1. Where possible, evaluate logarithmic expressions. log9x + log9y
log9x + log9y
A. log9y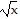
B. log9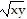
C. log9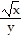
D. log9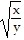
Evaluate 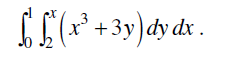
What will be an ideal response?