Use mathematical induction to prove that the statement is true for every positive integer n.5 + 5 ? 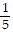 + 5 ?
+ 5 ? 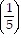 2 + . . . + 5 ?
2 + . . . + 5 ? 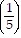 n - 1 =
n - 1 = 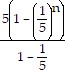
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. Then, 3 = 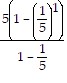 =
= 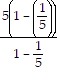 = 3. Thus, the statement is true for n = 1.
= 3. Thus, the statement is true for n = 1.
b). Assume that the statement is true for n = k:
Sk = 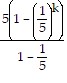
Also, if the statement is true for n = k + 1, then
Sk+1 = Sk + 5 ? 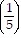 (k+1) - 1=
(k+1) - 1= 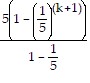
Substitute the expression for Sk into the one for Sk+1:
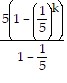 + 5 ?
+ 5 ? 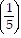 (k+1) - 1=
(k+1) - 1= 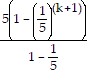
Collect the terms on the left-hand side over a common denominator:
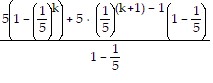 =
= 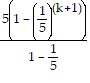
Expand the numerator of the left-hand side and simplify to get:
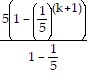 =
= 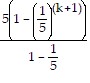
Since the equality holds, the statement is true for n = k + 1 as long as it is true for n = k. Furthermore, the statement is true for n = 1. Thus, the statement is true for all natural numbers n.
You might also like to view...
Solve the problem.Evaluate 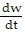 at t =
at t = 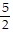 ? for the function w =
? for the function w = 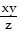 ; x = sin t, y = cost, z = t2.
; x = sin t, y = cost, z = t2.
A. - 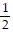
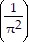
B. - 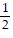
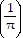
C. - 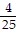
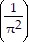
D. 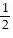
Suppose that the functions f and g and their derivatives with respect to x have the following values at the given values of x. Find the derivative with respect to x of the given combination at the given value of x.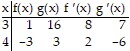
 , x = 3
, x = 3
A. - 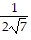
B. 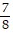
C. 
D. 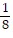
Solve the problem.A restaurant offered salads with 8 type(s) of dressing and 6 different topping(s). How many different types of salad could be ordered?
A. 36 B. 48 C. 64 D. 14
Find the particular solution to the given differential equation that satisfies the given conditions.Find the solution of the equation  if
if 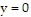 for
for  and
and  for
for 
A. y = b cos ax B. y = 0 C. y = b sin ax + b cos ax D. y = b sin ax