Use mathematical induction to prove the statement is true for all positive integers n.3 is a factor of n3 + 2n
What will be an ideal response?
Answers may vary. Possible answer:
First, we show the statement is true when n = 1.
For n = 1, 3 is a factor of 13 + 2 ? 1 = 3
So P1 is true and the first condition for the principle of induction is satisfied.
Next, we assume the statement holds for some unspecified natural number k. That is,
Pk: 3 is a factor of k3 + 2k is assumed true.
On the basis of the assumption that Pk is true, we need to show that Pk+1 is true.
Pk+1: 3 is a factor of (k + 1)3 + 2(k + 1).
(k + 1)3 + 2(k + 1) = (k3 + 3k2 + 3k + 1) + (2k + 2)
(k + 1)3 + 2(k + 1) = k3 + 2k + 3k2 + 3k + 3
(k + 1)3 + 2(k + 1) = (k3 + 2k) + 3(k2 + k + 1)
Since Pk is assumed true, 3 is a factor of (k3 + 2k) . Also 3 is a factor of 3(k2 + k + 1). So 3 is a factor of (k + 1)3 + 2(k + 1).
So Pk+1 is true if Pk is assumed true. Therefore, by the principle of mathematical induction, 3 is a factor of n3 + 2n for all natural numbers n.
You might also like to view...
Find the foci of the ellipse.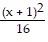 +
+ 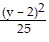 = 1
= 1
A. (-1, -2), (-1, 6) B. (-1, -1), (-1, 5) C. (-1, -3), (-1, 7) D. (-1, -1), (5, -1)
Translate the problem to a system of equations, then solve using Cramer's Rule.Twice the water flow in the hot-water pipe is the same as three times the flow in the cold-water pipe. The combined flow is 1300 liters per hour. What is the flow in each pipe?
A. 520 liters/hr hot, 780 liters/hr cold B. 433 liters/hr hot, 650 liters/hr cold C. 780 liters/hr hot, 520 liters/hr cold D. 650 liters/hr hot, 433 liters/hr cold
Find the equation of the transverse axis of the hyperbola.16(y + 1)2 - 9(x + 2)2 = 144
A. x = 2 B. x = -2 C. y = 1 D. x = -1
Factor the trinomial completely.4x3 - 32x2 + 60x
A. x(4x - 20)(x - 3) B. x(x - 5)(4x - 12) C. 4(x2 - 5x)(x - 3) D. 4x(x - 5)(x - 3)