A car is traveling on a curve that forms a circular arc. The force F needed to keep the car from skidding is jointly proportional to the weight w of the car and the square of its speed s, and is inversely proportional to the radius r of the curve. A car weighing 2,500 lbs travels around a curve at 70 mi/h. The next car to round this curve weighs 4,900 lbs and requires the same force as the first car to keep from skidding. How fast is the second car traveling?
 figure 1.png)
(b) 50 mi/h
You might also like to view...
Factor the trinomial, if possible.15x2 + 26x + 8
A. (15x + 1)(x + 8) B. (3x - 4)(5x - 2) C. (15x + 4)(x + 2) D. (3x + 4)(5x + 2)
Use long division to determine whether the binomial is a factor of f(x).f(x) = x4 - 10x3 + 35x2 - 50x + 24; x - 2
A. No B. Yes
Provide an appropriate response.The number of loaves of whole wheat bread left on the shelf of a local quick stop at closing (denoted by the random variable X) varies from day to day. Past records show that the probability distribution of X is as shown in the following table. Find the probability that there will be at least three loaves left over at the end of any given day.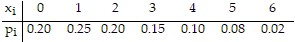 
A. 0.20 B. 0.65 C. 0.35 D. 0.15
Solve the problem.When a radioactive substance decays, the number N of grams remaining from an initial mass N0 (in grams) is given by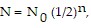 
where n is the number of half-lives for which the substance has decayed. Given that the half-life for tritium is 14 years, find the rate in (grams/half-life) at which a 102-gram initial mass of radioactive tritium decays after 44.8 years.
A. -70.7 g/half-life B. -11.1 g/half-life C. -7.69 g/half-life D. -3.38 g/half-life