Solve the problem.Let D be the region bounded below by the xy-plane, above by the sphere 
and on the sides by the cylinder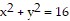 
. Set up the triple integral in cylindrical coordinates that gives the volume of D using the order of integration 
.
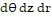A.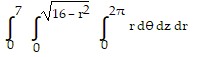 
B.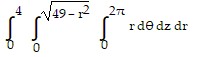 
C.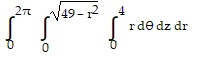 
D. 
Answer: B
You might also like to view...
Use a double-angle identity to find the exact value of the expression.2 cos2 22.5° - 1
A.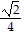 
B.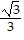 
C.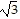 
D.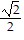 
Consider the points plotted in the graph below.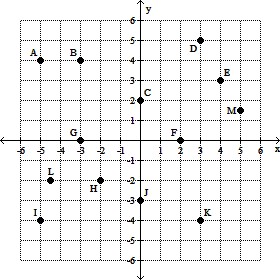
Give the coordinates for point K.
A. (-4, 3) B. (3, -4) C. (3, 4) D. (4, 3)
Simplify the expression. Assume that all variables are positive when they appear.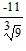
A. -11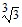
B. -11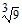
C.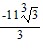 
D. 
Identify the problem with the method used to obtain a random sample.A quality control manager would like to assess the quality of service provided by one of his customer service representatives. He would like to listen to a random sample of calls handled by the representative. He monitors the first 30 calls handled by the representative on a Monday morning.
A. The day Monday was not chosen at random. The manager should write each day of the week on a slip of paper, put the slips in a bag, mix them thoroughly, close his eyes and pick a slip from the bag. He should then monitor the first 30 calls handled by the representative on the day selected. B. The manager cannot pick a random sample because he is not objective. Someone other than the manager should select the calls to be monitored. C. The sample is biased. Calls handled at times other than Monday morning have no chance of being selected. The first 30 calls handled on a Monday morning might not be representative of all calls handled by the representative.. If the representative happened to be tired or in a bad mood on the Monday morning this would affect all calls in the sample.