Solve the problem.Suppose that R and C play a game by matching coins. If R shows "heads" and C shows "tails", C pays R $2. If R shows "tails" and C shows "heads", R pays C $1. If they both show "heads", C pays R $1. If they both show "tails", R pays C $2.(a) Give the payoff matrix for this game.(b) Decide if the game is strictly determined. If so, determine the optimal strategies for R and C.
What will be an ideal response?
| (a) | C |
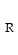
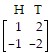
| (b) | strictly determined; R shows "heads", C shows "heads" |
Mathematics
You might also like to view...
Solve. Give your answer as a mixed number if appropriate. =
= 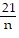
A. 
B. 12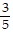
C. 35
D. 105
Mathematics
Solve the equation for y in terms of x.ln y + 2 ln x = 1 + ln 9
A. y = 10 - 2x
B. y = e + 9 - 2x
C. y = 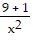
D. y = 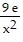
Mathematics
Express the integrand as a sum of partial fractions and evaluate the integral.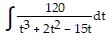
A. - 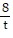 + 5ln
+ 5ln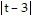 + 3ln
+ 3ln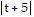 + C
+ C
B. -8 ln 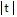 + 5ln
+ 5ln + C
+ C
C. -3 ln 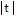 + 5ln
+ 5ln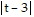 - 3ln
- 3ln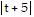 + C
+ C
D. -8 ln 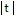 + 5ln
+ 5ln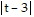 + 3ln
+ 3ln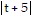 + C
+ C
Mathematics
Find the equation of variation if the following is true.Suppose m varies directly as p and m = 20 when p = 4.
A. m = 16p
B. m = 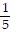 p
p
C. m = 24p
D. m = 5p
Mathematics