For each integer n ? 3, let P(n) be the equation
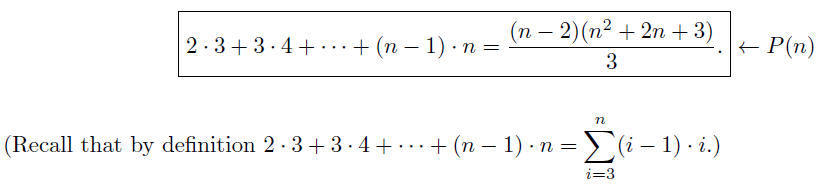
(a) Is P(3) true? Justify your answer.
(b) In the inductive step of a proof that P(n) is true for all integers n ? 3, we suppose P(k) is true (this is the inductive hypothesis), and then we show that P(k + 1) is true. Fill in the blanks below to write what we suppose and what we must show for this particular equation.
Proof that for all integers k ? 3, if P(k) is true then P(k + 1) is true:
Let k be any integer that is greater than or equal to 3, and suppose that __________.
We must show that __________.
(c) Finish the proof started in (b) above.
You might also like to view...
Solve the problem.The shape and density of a thin shell are indicated below. Find the coordinates of the center of mass.Shell: portion of the sphere x2 + y2 + z2 = 25 that lies in the first octantDensity: constant
A.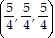 
B. 
C. 
D. 
Plot the indicated graphs.On a certain moon, the distance s (in ft) a rock will fall due to gravity is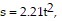 
where t is the time (in s) of fall. Plot the graph of s as a function of t for 
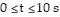on semilogarithmic graph paper.
What will be an ideal response?
Write the slope-intercept form of the equation for the line passing through the given pair of points.(-7, 1) and (6, 3)
A. y =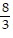 
x + 19
B. y = 
x + 
C. y = - 
x + 
D. y = -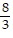 
x + 19
Evaluate the function.Given f(x) = x2 - 5x - 1, find f(-2).
A. 15 B. -7 C. 13 D. -5