Provide an appropriate response.Show that the function f(x) = x3 +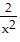 
+ 8 has exactly one zero on the interval (-?, 0).
What will be an ideal response?
The function f(x) is continuous on the open interval (-?, 0). Also, f(x) approaches -? as x approaches -?, and f(x) approaches ? as x approaches 0 from the left. Since f(x) is continuous and changes sign along the interval, it must have at least one root on the interval.
The first derivative of f(x) is f'(x) = 3x2 -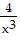 
, which is everywhere positive on (-?, 0). Thus, f(x) has a single root on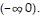 
You might also like to view...
Solve the absolute-value inequality.|r + 9| > 5
A. {r
-14 < r < -4}, or (-14, -4)
B. ?
C. {r
r < -14 or r > -4}, or (-?, -14) ? (-4, ?)
D. {r
r > -4}, or (-4, ?)
Form a tiling from the given figure using translations and reflections.
What will be an ideal response?
Simplify the following. Leave answer as a power.313 ? 3033 ? 1013
A. 3046 B. None of these C. 3033 ? 1026 D. 3033 ? 1013
Write an equation for a function whose graph fits the given description.The graph of f(x) =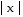 
is reflected across the y-axis. This graph is then vertically stretched by a factor of 3.1. Finally, the graph is shifted 2 units downward.
A. f(x) = 3.1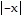
+ 2
B. f(x) = 3.1
- 2
C. f(x) = 2
- 3.1
D. f(x) = -3.1
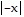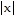- 2