Mark as true any statement that is always true. Mark as false any statement that is never true or that is not necessarily true. Be able to justify your answers.
1. If a statement is true then its contrapositive must also be true.
2. If p ? q and q ? r then r ? p.
3. The statement “if p then q” can be read as “q only if p.”
4. If a statement is false, then its converse must also be false.
5. If ?MAD ? ?ROC, then ?DMA ? ?ORC.
6. If two triangles are congruent, then there are exactly three pairs congruent parts—the corresponding angle pairs.
7. In ABC, if AB ? BC then ?BAC ? ?ACB.
8. If AB ? XY , BC ? YZ and ?ABC ? ?XYZ then ?ABC ? ?XYZ
9. In ABC, ABC CBA by corresponding parts (C.P.)
10. If PQ bisects AB, then AP ? BP.
11. To construct a copy of AB, we begin by drawing a new line.
12. The construction of a perpendicular bisector of a segment requires three arcs and one line.
13. The construction of the bisector of an angle requires three arcs and one line.
1. T
2. F: This is the converse of the correct statement p r.
3. F—”if p then q” is the same as “p only if q.”
4. F—A statement and it converse may or may not have the same truth value.
5. T
6. F: There are six pairs of congruent parts.
7. T
8. F: SSA is not a valid congruence condition.
9. F: By Identity
10. F— PQ must be perpendicular to AB to reach the conclusion.
11. T
12. T
13. T
You might also like to view...
Use partial derivatives to find the implicit derivative  figures 4.png) .
.
 figure.png)
Simplify.3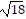 - 5
- 5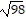
A. 26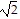
B. -26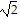
C. -44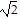
D. 44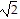
Determine whether the lines through each pair of points are perpendicular.(4, -9) and (-12, -7); (3, -8) and (2, -16)
A. perpendicular B. not perpendicular
Solve the system by graphing. If there is no solution or an infinite number of solutions, so state. Use set notation to express the solution set.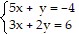

A. {(2, 6)} B. {(-2, -3)} C. {(-2, 6)} D. {(0, -4)}