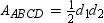Use the drawing provided to explain the following theorem.“The area of any quadrilateral with perpendicular diagonals of lengths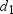 
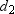
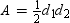
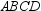
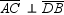
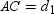
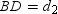
and 
is given by
.”Given: Quadrilateral 
with 
at point F; 
and 
Prove: 
What will be an ideal response?
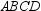, we draw auxiliary lines as follows:through point D, we draw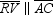 
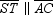
; through point B, we draw 
;
through point A, we draw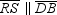 
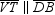
; and through point C, we draw 
.
The quadrilateral formed is a parallelogram that can be shown to have a right angle;
this follows from the fact that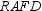 
is a parallelogram that contains a right angle at
vertex F . . . so the opposite angle (at vertex R) must also be a right angle.
Because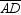 
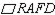
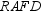
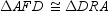
is a diagonal of 
(actually rectangle 
, 
;
that is, a diagonal of a parallelogram separates the parallelogram into 2 congruent 
.
Similarly,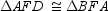 
, 
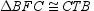
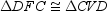
, and 
. Thus, the area
of quadrilateral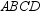 
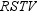
is one half of that of rectangle 
.
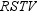
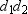
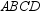
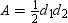
But the area of is 
, so 
is given by 
.
You might also like to view...
Choose the ordered pair which is a solution of the inequality.2x + 3y < 5
A. (1, 1)
B. (2, 2)
C.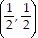 
D. (3, 2)
Solve.Find the angle, 2x, in the wedge shown. Round to the nearest tenth.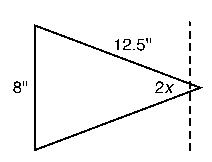
Fill in the blank(s) with the appropriate word(s).
Solve by the elimination method:
10x + 39y = 16
15x + 39y = 18
Solve the problem.Economists use what is called a Leffer curve to predict the government revenue for tax rates from 0% to 100%. Economists agree that the end points of the curve generate 0 revenue, but disagree on the tax rate that produces the maximum revenue. Suppose an economist produces this rational function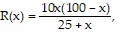 
where R is revenue in millions at a tax rate of x percent. Use a graphing calculator to graph the function. What tax rate produces the maximum revenue? What is the maximum revenue?
A. 28.8%; $272 million B. 27.0%; $379 million C. 30.9%; $382 million D. 38.4%; $383 million