A company has the Cobb-Douglas production function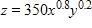 
, where x is the number of units of labor, y is the number of units of capital, and z is the units of production. Suppose labor costs $200 per unit, capital costs $150 per unit, and the total cost of labor and capital is limited to $300,000. Find the number of units of labor and the number of units of capital that maximize production.
?
A. 1,500 units of labor; 2,000 units of capital
B. 1,200 units of labor; 2,000 units of capital
C. 1,500 units of labor; 400 units of capital
D. 1,200 units of labor; 400 units of capital
E. 12,000 units of labor; 4,000 units of capital
Answer: D
You might also like to view...
A graph can show where a function is increasing.
Answer the following statement true (T) or false (F)
Solve the problem.Determine whether (1, 4, -2) is a solution of the systemx + y + z = 3 x - y + 4z = -114x + y + z = 6
A. No B. Yes
Find the LCM of the set of numbers.14, 12
A. 336 B. 168 C. 2 D. 84
Write the decimal using the indicated form.5.008694; expanded exponential form
A. 5 ? 100 + 0 ? 101 + 0 ? 102 + 8 ? 103 + 6 ? 104 + 9 ? 105 + 4 ? 106 B. 5 ? 101 + 0 ? 100 + 0 ? 10-1 + 8 ? 10-2 + 6 ? 10-3 + 9 ? 10-4 + 4 ? 10-5 C. 5 ? 100 + 0 ? 10-1 + 0 ? 10-2 + 8 ? 10-3 + 6 ? 10-4 + 9 ? 10-5 + 4 ? 10-6 D. 5 ? 100 + 8 ? 10-1 + 6 ? 10-2 + 9 ? 10-3 + 4 ? 10-4