Consider the statement
For all sets A and B, (A ? B) ? B = ?.
Complete the proof begun below in which the given statement is derived algebraically from the properties listed in Theorem 6.2.2. Be sure to give a reason for every step that exactly justifies what was done in the step:
Proof:
Let A and B be any sets. Then the left-hand side of the equation to be shown is
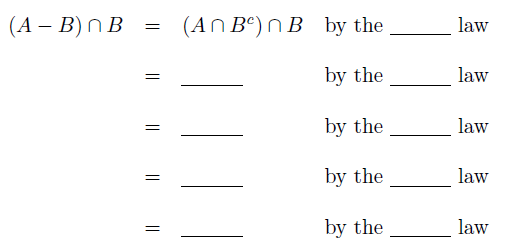
which is the right-hand side of the equation to be shown. [Hence the given statement is true.]
(The number of lines in the outline shown above works for one version of a proof. If you write a proof using more or fewer lines, be sure to follow the given format, supplying a reason for every step that exactly justifies what was done in the step.)
You might also like to view...
Use the slopes of UQ, UR, US, and UT to estimate the rate of change of y at the specified value of x.x = 5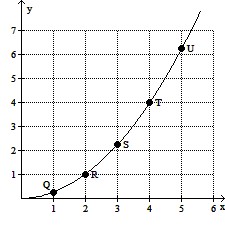
A. 0
B.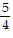 
C.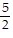 
D.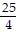 
Express the limit as a definite integral.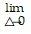
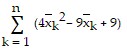?xk; [-2, 3]
A.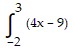 
dx
B. 
dx
C. 
dx
D. 
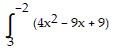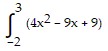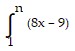dx
Determine whether the relation represents a function. If it is a function, state the domain and range.{(5.44, 8.54), (5.444, -8.5), (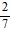
, 0), (0.29, -5)}
A. function
domain: {5.44, 5.444, 
, 0.29}
range: {8.54, -8.5, 0, -5}
B. function
domain: {8.54, -8.5, 0, -5}
range: {5.44, 5.444,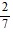 
, 0.29}
C. not a function
Solve the problem.The graph depicts a person's speed y, in miles per hour, during a 15-minute period of driving. Estimate and interpret the turning points.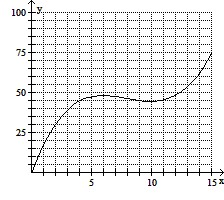
A. The first turning point is at approximately (6, 48). This is where the person's speed first stops increasing and starts to decrease. The second turning point is at approximately 
. This is where the person's speed stops decreasing and starts to increase again.
B. The first turning point is at approximately (7, 48). This is where the person's speed first stops increasing and starts to decrease. The second turning point is at approximately (11, 44). This is where the person's speed stops decreasing and starts to increase again.
C. The first turning point is at approximately (5, 48). This is where the person's distance from the starting point stops increasing and starts to decrease. The second turning point is at approximately (9, 44). This is where the person's distance from the starting point stops decreasing and starts to increase again.
D. The first turning point is at approximately (6, 48). This is where the person's distance from the starting point stops increasing and starts to decrease. The second turning point is at approximately (10, 44). This is where the person's distance from the starting point stops decreasing and starts to increase again.