Use mathematical induction to prove that the statement is true for every positive integer n.6n > n
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. Then, 31 = 3 > 1, so the statement is true for n = 1.
b). Assume that the statement is true for n = k:
3k > k
Multiply both sides by 3:
3?3k = 3k+1 > 3k
Also, since k ? 1, then 2k > 1, which can be re-written as 3k > k + 1. Thus,
3k+1 > k + 1
Since the statement is true for n = k + 1 as long as it is true for n = k, and since the statement is true for n = 1, then it is true for all natural numbers n.
You might also like to view...
Find the volume.Find the volume of a cone with height 5 inches and radius 8 inches Use 3.14 for ?. Round to the nearest whole number.
A. 335 in3 B. 670 in3 C. 502 in3 D. 84 in3
Factor the expression completely, if possible.x4 - 27x
A. x(x + 3)(x2 - 3x + 9) B. (x2 - 3)(x2 + 9) C. x(x - 3)(x2 + 3x + 9) D. Does not factor
Use the definition or identities to find the exact value of the indicated trigonometric function of the acute angle ?.tan ? = 2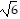 Find the remaining five trigonometric functions of the acute angle ?.
Find the remaining five trigonometric functions of the acute angle ?.
What will be an ideal response?
Solve the problem.Round 24,711,373 to the nearest million.
A. 24,800,000 B. 25,000,000 C. 24,000,000 D. 24,711,000