Use mathematical induction to prove that the statement is true for every positive integer n.4 ? 6 + 5 ? 7 + 6 ? 8 + . . . + (n + 3)(n + 5) = 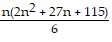
What will be an ideal response?
Answers will vary. One possible proof follows.
a). Let n = 1. Then, 4 ? 6 = 8 = 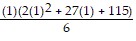 =
= 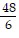 = 8. Thus, the statement is true for n = 1.
= 8. Thus, the statement is true for n = 1.
b). Assume that the statement is true for n = k:
Sk = 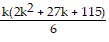
Also, if the statement is true for n = k + 1, then
Sk+1 = Sk + ((k + 1) + 3)((k + 1) + 5) = 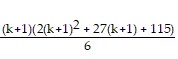
Substitute the expression for Sk into the one for Sk+1:
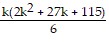 + ((k + 1) + 3)((k + 1) + 5) =
+ ((k + 1) + 3)((k + 1) + 5) = 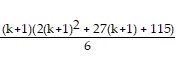
By collecting all terms on the left-hand side over a common denominator and then expanding numerators on both sides, one can show that the equality holds.
Since the equality holds, the statement is true for n = k + 1 as long as it is true for n = k. Furthermore, the statement is true for n = 1. Thus, it is true for all natural numbers n.
You might also like to view...
Tell whether the statement is true or false.{s, q, y, o, d} = {o, d, q, s, y}
A. True B. False
Determine the average rate of change for the function.F(x) = -7
A. 7
B. 0
C. - 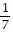
D. -7
Solve the inequality. Express your answer using interval notation. Graph the solution set.|x| < 4![]()
A. (-?, -4) ? (4, ?)![]()
B. (-?, 4]![]()
C. [-4, 4]![]()
D. (-4, 4)![]()
Find the solution(s) (if any) of the system of equations by the graphical method. If the equations are dependent, write your answer with x being arbitrary.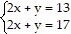
A. {(x, 13 - 2x)} B. inconsistent C. {(10, -7)} D. {(6, 7)}