A pharmaceutical company produces three kinds of cold formulas: I, II, and III. It takes 2 hr to produce 1,000 bottles of formula I, 4 hr to produce 1,000 bottles of formula II, and 3 hr to produce 1,000 bottles of formula III. The profits for each 1,000 bottles of formula I, formula II, and formula III are $220, $130, and $190, respectively. Suppose, for a certain production run, there are enough ingredients on hand to make at most 7,000 bottles of formula I, 17,000 bottles of formula II, and 9,000 bottles of formula III. Furthermore, suppose the time for the production run is limited to a maximum of 100 hr. How many bottles of each formula should be produced in this production run so that the profit is maximized?
__________ bottles of formula I,
__________ bottles of formula II,
__________ bottles of formula III
What is the maximum profit realizable by the company? $ __________
Are there any resources left over?
ingredients for __________ bottles of formula I,
ingredients for __________ bottles of formula II,
ingredients for __________ bottles of formula III,
__________ hr of the time for the production run
7,000;14,750;9,000;5,167.50;0;2,250;0;0
You might also like to view...
Evaluate. The differential is exact.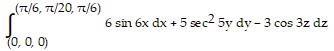
A. 1 B. 4 C. 2 D. 0
Solve the problem.The sum of three consecutive odd integers is 195. Find the integers.
A. 58, 59, 60 B. 65, 67, 69 C. 63, 65, 67 D. 67, 69, 71
Use the FOIL method to find the product.(x - 11)(5x - 9)
A. x2 - 64x - 64 B. 5x2 - 64x + 99 C. 5x2 - 65x + 99 D. 5x2 + 99x - 64
Find a rational function that satisfies the given conditions. Answers may vary, but try to give the simplest answer possible.Vertical asymptotes x = -5, x = -2
A. f(x) = 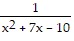
B. f(x) = 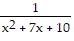
C. f(x) = 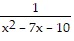
D. f(x) = 