Consider player n in a sequential game.
a. If the player can play 3 actions from a single node, how many pure strategies does he have?
b. Suppose he can play 3 actions at each of two different nodes. How many pure strategies does he have now?
c. Suppose he can play 3 actions at each of three different nodes. How many pure strategies does he have now?
d. Suppose he can play 3 actions at each of four different nodes. How many pure strategies does he have now?
e. Suppose he can play 3 actions at each of k different nodes. How many pure strategies does he have now?
What will be an ideal response?
a. He simply chooses one of his 3 actions -- and thus has 3 possible strategies.
b. Suppose the actions at each node are L, M and R. Then his strategies are (L,L), (L,R), (R,L), (R,R), (M,L), (L,M), (M,M), (M,R), (R,M) -- so he has 9 possible strategies.
c. We now have to specify an action for each of 3 nodes. The portions of the strategies for the last two nodes are the same as the strategies in (b) -- but now he combines those with playing L, M or R in the first stage. Thus, we now have 27 possible strategies.
d. The portions of the strategies for the last 3 nodes are now the same as the strategies if there were only 3 nodes -- i.e. there are 27 of those (as determined in (c)). But now the player has to combine these with either L, M or R in the first stage -- giving us 81 possible strategies.
e. Following the pattern developed in (a) through (d), the number of strategies is now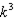 .
.
b. Suppose the actions at each node are L, M and R. Then his strategies are (L,L), (L,R), (R,L), (R,R), (M,L), (L,M), (M,M), (M,R), (R,M) -- so he has 9 possible strategies.
c. We now have to specify an action for each of 3 nodes. The portions of the strategies for the last two nodes are the same as the strategies in (b) -- but now he combines those with playing L, M or R in the first stage. Thus, we now have 27 possible strategies.
d. The portions of the strategies for the last 3 nodes are now the same as the strategies if there were only 3 nodes -- i.e. there are 27 of those (as determined in (c)). But now the player has to combine these with either L, M or R in the first stage -- giving us 81 possible strategies.
e. Following the pattern developed in (a) through (d), the number of strategies is now
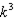 .
.
Economics
You might also like to view...
Rent seeking is devoted to the creation of
A) monopolies. B) competitive industries. C) human capital. D) more elastic demand.
Economics
Which of the following policy actions by the Fed would cause the money supply to decrease?
a. A decrease in required reserve ratios. b. An open-market purchase of government securities. c. A decrease in the discount rate. d. An increase in the discount rate.
Economics
Using Table 6.1, from the 1982-1984 base to 2004, prices increased 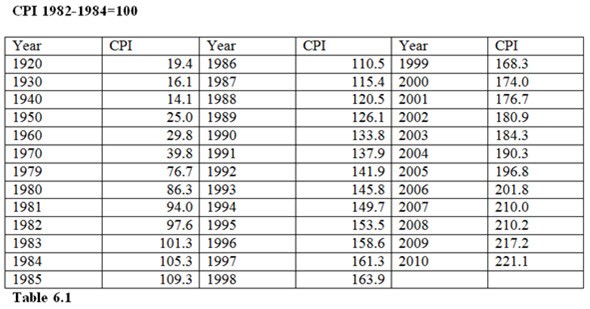
A. by 90.3 dollars per week on monthly bills. B. 90.3%. C. 190.3%. D. 90.3 times.
Economics
The Five Forces Model determines whether an industry is an oligopoly.
Answer the following statement true (T) or false (F)
Economics