Solve the problem.A product of two oscillations with different frequencies such as f(t) = sin(10t) sin(t)is important in acoustics. The result is an oscillation with "oscillating amplitude."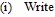 the product f(t) of the two oscillations as a sum of two cosines and call it g(t).
the product f(t) of the two oscillations as a sum of two cosines and call it g(t). a graphing utility, graph the function g(t) on the interval 0 ? t ? 2?.
a graphing utility, graph the function g(t) on the interval 0 ? t ? 2?. the same system as your graph, graph y = sin t and y = -sin t.
the same system as your graph, graph y = sin t and y = -sin t.
src="https://sciemce.com/media/4/ppg__tttt0506191043__f1q58g4.jpg" alt="" style="vertical-align: -4.0px;" /> last two functions constitute an "envelope" for the function g(t). For certain values of t, the two cosine functions in g(t) cancel each other out and near-silence occurs; between these values, the two functions combine in varying degrees. The phenomenon is known (and heard) as "beats." For what values of t do the functions cancel each other?
What will be an ideal response?
(i) g(t) = 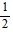 cos(9t) -
cos(9t) - 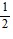 cos(11t)
cos(11t)
(ii), (iii)
(iv) t = 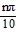 , n any integer
, n any integer
Mathematics
src="https://sciemce.com/media/4/ppg__tttt0506191043__f1q58g4.jpg" alt="" style="vertical-align: -4.0px;" /> last two functions constitute an "envelope" for the function g(t). For certain values of t, the two cosine functions in g(t) cancel each other out and near-silence occurs; between these values, the two functions combine in varying degrees. The phenomenon is known (and heard) as "beats." For what values of t do the functions cancel each other?
What will be an ideal response?
| (i) | g(t) = 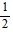 cos(9t) - cos(9t) - 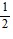 cos(11t) cos(11t) |

(iv) t =
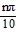 , n any integer
, n any integerYou might also like to view...
Determine whether the Fourier series of the given function will include only sine terms, only cosine terms, or both sine terms and cosine terms.f(x) = 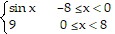
A. only sine terms B. only cosine terms C. both sine and cosine terms
Evaluate.Let a = 3i, b = i + j. Find 6a - b.
A. 17i - j B. i - 17j C. 11i + j D. 17i - 6j
Multiply.(8x + 7y)(8x - 7y)
A. 64x2 - 112xy - 49y2 B. 64x2 - 49y2 C. 64x2 + 112xy - 49y2 D. 64x2 + 49y2
If the perimeter of ?ABC is 24 cm, find the length of each side.
