Prove the following statement directly from the definitions of the terms. Do not use any other facts previously proved in class or in the text or in the exercises.
For all integers a, b, and c, if a | b and a | c, then a | (5b + 3c).
Proof : Suppose a, b, and c are any integers such that a | b and a | c. [We must show that a | (5b+3c).]
By definition of divisibility, b = ar and c = as for some integers r and s. Then
5b + 3c = 5(ar) + 3(as) by substitution
= a(5r + 3s) by the commutative and associative laws of algebra.
Let t = 5r+3s. Then t is an integer because products and sums of integers are integers, and 5b+3c = at.
Thus, by definition of divisibility, a | (5b + 3c) [as was to be shown].
Prove the following statement directly from the definitions of the terms. Do not use any other facts
previously proved in class or in the text or in the exercises.
For all integers a; b; and c; if a | b and a | c; then a | (5b + 3c):
You might also like to view...
Solve.8x(x - 2) - 20 = 5x(x - 4)
A. - 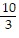 , 2
, 2
B. -10, 2
C. - 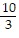 , -2
, -2
D. 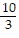 , -2
, -2
Round the whole number to the given place value.35, tens
A. 40 B. 50 C. 30 D. 43
Provide an appropriate response.The number of loaves of whole wheat bread left on the shelf of a local quick stop at closing (denoted by the random variable X) varies from day to day. Past records show that the probability distribution of X is as shown in the following table. Find the probability that there will be at least three loaves left over at the end of any given day. 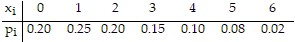
A. 0.20 B. 0.65 C. 0.35 D. 0.15
Subtract.775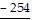
A. 421 B. 513 C. 1029 D. 521