Find the unit tangent vector T and the principal unit normal vector N. r(t) = (cosh t)i + (sinh t)j + tk
A. T = - 
(tanh t sech t)i + 
j + 
(sech t)k; N = (-sech t)i - (tanh t)k
B. T = -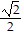 
(tanh t)i + 
j + 
(sech t)k; N = (-sech t)i - (sinh t)k
C. T =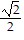 
(tanh t)i + 
j + 
(sech t)k; N = (sech t)i - (tanh t)k
D. T = 
(tanh t sech t)i + 
j + 
(sech t)k; N = (sech2 t)i - (sinh t)k
Answer: C
You might also like to view...
Find the slope of the line that goes through the given points.(-9, -7), (-3, 9)
A. -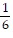 
B. -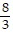 
C.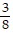 
D.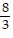 
Solve the problem.The sum of three numbers is -4. If the second number is subtracted from the sum of the first and third numbers, the result is 4. If the third number is subtracted from the sum of the first and second numbers, the result is 6. Find the three numbers.[Hint: let x represent the first number, y the second number, and z the third number. Use the given conditions to write and solve a system of equations.]
A. x = 6, y = -4, z = -6 B. x = 5, y = -4, z = -5 C. x = 3, y = -2, z = -5 D. x = 6, y = -3, z = -7
Determine the integral by making an appropriate substitution.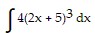
A.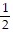 
(2x + 5)4 + C
B.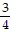 
(2x + 5)4 + C
C.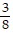 
(2x + 5)4 + C
D.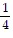 
(2x + 5)4 + C
Solve the equation. If the equation is an identity or a contradiction, state this.6(x + 6) - 2(x + 6) = 4x + 24
A. all real numbers; identity B. {-1} C. ? or { }; contradiction D. {6}