Use the precise definition of a limit to prove the limit. Specify a relationship between ? and ? that guarantees the limit exists. x4 = 16
x4 = 16
A. ? = min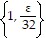 ; Let ? > 0 and assume 0 <
; Let ? > 0 and assume 0 <  < ?. Then
< ?. Then  =
= 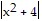
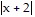
 =
=  That is, for any ? > 0,
That is, for any ? > 0,  = ? whenever 0 <
= ? whenever 0 <  < ?, provided 0 < ? ?
< ?, provided 0 < ? ?  . Therefore,
. Therefore,  x4 = 16.
x4 = 16.
B. ? = min ; Let ? > 0 and assume 0 <
; Let ? > 0 and assume 0 <  < ?. Then
< ?. Then 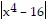 =
= 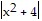

 =
=  That is, for any ? > 0,
That is, for any ? > 0,  = ? whenever 0 <
= ? whenever 0 <  < ?, provided 0 < ? ?
< ?, provided 0 < ? ?  . Therefore,
. Therefore,  x4 = 16.
x4 = 16.
C. ? = min 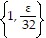 ; Let ? > 0 and assume 0 <
; Let ? > 0 and assume 0 <  < ?. Then
< ?. Then  =
= 

 <
< 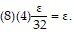 That is, for any ? > 0,
That is, for any ? > 0,  < ? whenever 0 <
< ? whenever 0 <  < ?, provided 0 < ? ?
< ?, provided 0 < ? ?  . Therefore,
. Therefore, 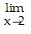 x4 = 16.
x4 = 16.
D. ? = min  ; Let ? > 0 and assume 0 <
; Let ? > 0 and assume 0 < 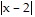 < ?. Then
< ?. Then 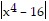 =
= 
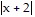
 <
< 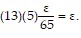 That is, for any ? > 0,
That is, for any ? > 0, 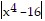 < ? whenever 0 <
< ? whenever 0 <  < ?, provided 0 < ? ?
< ?, provided 0 < ? ?  .
.
Therefore, 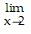 x4=16.
x4=16.
Answer: D
You might also like to view...
Find a set of polar coordinates for the point for which the rectangular coordinates are given.(-3, 0)
A. 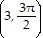
B. (3, 0)
C. (3, ?)
D. 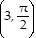
Solve.A ladder that is 15 feet long is 9 feet from the base of a wall. How far up the wall does the ladder reach?
A. 12 ft
B. 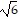 ft
ft
C. 144 ft
D. 3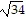 ft
ft
Subtract.79,777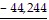
A. 35,533 B. 35,525 C. 39,533 D. 35,445
Find the center of the ellipse. 4(x + 1)2 + 16(y + 4)2 = 64
A. (-1, -4) B. (-4, -1) C. (1, 4) D. (4, 16)