Use a table of values to graph the plane curve defined by the following parametric equations. Find a rectangular equation for the curve.x = 8 sin t, y = 8 cos t, for t in [0, 2?] 
A. 
y = x2 - 9, for x in [-2, 2]
B. 
y =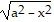 
= 64, for x in [-8, 8]
C. 
x2 + y2 = 64, for x in [-8, 8]
D. 
y2 - x2 = 64, for x in [-8, 8]
Answer: C
You might also like to view...
Give a number that satisfies the given condition.A whole number greater than 3.5
What will be an ideal response?
Find all the factors of the natural number.63
A. 1, 3, 5, 7, 9, 11, 21, 63 B. 1, 2, 3, 7, 9, 21, 36, 63 C. 3, 5, 7, 9, 11, 21, 63 D. 1, 3, 7, 9, 21, 63
Find the vertical asymptotes of the rational function.g(x) = 
A. x = 9, x = -11 B. x = 0, x = 9 C. x = -3, x = 3 D. x = 0, x = -3, x = 3
Interpret the linear equation.The altitude above sea level of an airplane just after taking off from an airport on a high plateau is given by the linear function y = 400x + 2992, where y is in feet and x is the time in minutes since take-off. Find and interpret the slope and y-intercept.
A. m = 400; The minutes since take-off increases 400 for every foot of altitude.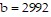 
; The minutes that the plane takes to get to the altitude of the airport from sea level.
B. m = 2992; The minutes since take-off increases 2992 for every foot of altitude.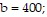 
The minutes that the plane takes to get to the altitude of the airport from sea level.
C. m = 400; The altitude of the airplane increases 400 feet every minute. b = 2992; The altitude of the airport where the airplane took-off is 2992 feet above sea level.
D. m = 2992; The altitude of the airplane increases 2992 feet every minute. b = 2992; The altitude of the airport where the airplane took-off is 400 feet above sea level.