Solve the problem.A certain developing country has a population of 500,000. The yearly rate of increase of literacy among the people is proportional to the number of illiterate people in the population. Letting f(t) represent the number of literate people, determine the differential equation that f(t) satisfies. (Let k represent a positive constant.)
A. f'(t) = 500,000 - kf( t)
B. f'(t) = 
C. f'(t) = k(500,000 - f(t))
D. f'(t) = 500,000(1 - f(t))
E. none of these
Answer: C
You might also like to view...
Provide an appropriate response.If 
and 
both converge conditionally, what can be said about 
?
A. The series always diverges. B. The series always converges. C. The series may converge or diverge.
Solve the problem. Round to tenths where necessary.A bookstore has an annual demand for 78,000 copies of a best-selling book. It costs $0.5 to store one copy for one year, and it costs $55 to place an order. Find the optimum number of copies per order.
A. 3728 copies B. 5858 copies C. 4142 copies D. 5000 copies
Solve the problem.141 students attended an assembly at Piper School. The student enrollment at the school is 564. What percentage of the students did not attend the assembly?
A. 75% B. 70% C. 60% D. 85%
Graph the polar equation.r = 1 - 3 cos ?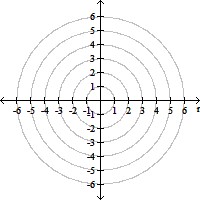
A.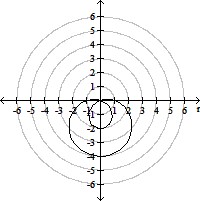 
B.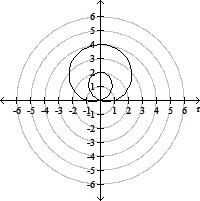 
C.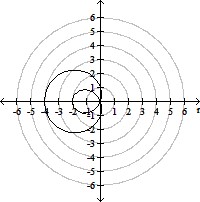 
D. 