Solve the problem.The rate of expenditure on a particular machine is given by dM/dx = 9x , where x is time measured in years. Maintenance costs for the second year are $74. Find the total maintenance function, M.
, where x is time measured in years. Maintenance costs for the second year are $74. Find the total maintenance function, M.
A. M = 3(x2 + 5)3/2 + 65
B. M = 9(x2 + 5)3/2 - 7
C. M = 9(x2 + 5)3/2 + 65
D. M = 3(x2 + 5)3/2 - 7
Answer: D
You might also like to view...
The associative and commutative properties for addition allow for three or more integers to be added in any order. Find the given sum.-7 + (-5) + (-10)
A. -12 B. 2 C. -22 D. 8
Solve the problem.A small farm field is a square measuring 200 ft on a side. What is the perimeter of the field?
A. 200 ft B. 800 ft C. 1600 ft D. 400 ft
Use the graph to solve the problem.Find the rate of change in the height of the tree.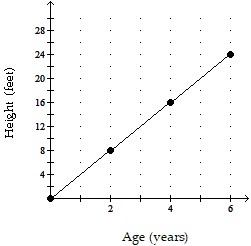
A. 10 feet per year B. 4 feet per year C. 8 feet per year D. 2 feet per year
A sausage company makes two different kinds of hot dogs, regular and all beef. Each pound of all-beef hot dogs requires 0.75 lb of beef and 0.2 lb of spices, and each pound of regular hot dogs requires 0.18 lb of beef, 0.3 lb of pork, and 0.2 lb of spices. Suppliers can deliver at most 1,020 lb of beef, at most 600 lb of pork, and at least 500 lb of spices. If the profit is $0.70 on each pound of all-beef hot dogs and $0.40 on each pound of regular hot dogs, how many pounds of each should be produced to obtain maximum profit? What is the maximum profit? Round your profit to the nearest cent, another answers - to the nearest wholenumber. ?
A. Maximum profit of $1150.00 with 2000 lbs of regular and 500 lbs of all beef. B. Maximum profit of $1416.00 with 2000 lbs of regular and 880 lbs of all beef. C. Maximum profit of $1752.00 with 880 lbs of regular and 2000 lbs of all beef. D. Maximum profit of $1300.00 with 1500 lbs of regular and 1000 lbs of all beef. E. Maximum profit of $1450.00 with 1000 lbs of regular and 1500 lbs of all beef.